The 11 Most Beautiful Mathematical Equations

[Ichingcarpenter]

Mathematical equations aren't just useful — many are quite beautiful. And many scientists admit they are often fond of particular formulas not just for their function, but for their form, and the simple, poetic truths they contain.

While certain famous equations, such as Albert Einstein's E = mc^2, hog most of the public glory, many less familiar formulas have their champions among scientists. LiveScience asked physicists, astronomers and mathematicians for their favorite equations; here's what we found:
General relativity

The equation above was formulated by Einstein as part of his groundbreaking general theory of relativity in 1915. The theory revolutionized how scientists understood gravity by describing the force as a warping of the fabric of space and time.

"It is still amazing to me that one such mathematical equation can describe what space-time is all about," said Space Telescope Science Institute astrophysicist Mario Livio, who nominated the equation as his favorite. "All of Einstein's true genius is embodied in this equation." [Einstein Quiz: Test Your Knowledge of the Genius]
"The right-hand side of this equation describes the energy contents of our universe (including the 'dark energy' that propels the current cosmic acceleration)," Livio explained. "The left-hand side describes the geometry of space-time. The equality reflects the fact that in Einstein's general relativity, mass and energy determine the geometry, and concomitantly the curvature, which is a manifestation of what we call gravity." [6 Weird Facts About Gravity]

"It's a very elegant equation," said Kyle Cranmer, a physicist at New York University, adding that the equation reveals the relationship between space-time and matter and energy. "This equation tells you how they are related — how the presence of the sun warps space-time so that the Earth moves around it in orbit, etc. It also tells you how the universe evolved since the Big Bang and predicts that there should be black holes."


To read the list of the 11 go to the link:

http://news.yahoo.com/11-most-beautiful-mathematical-equations-144744064.html;_ylt=Aj1x_BvsW0k7C91OQ5hc1Zu1qHQA;_ylu=X3oDMTQxN3JkdGdlBG1pdANNb3N0UG9wdWxhciBMaXN0aW5nBHBrZwMwOGM1ZjRhZi0wZTRlLTMyMmMtYTQ0NS1kN2JkODM3N2JlNzEEcG9zAzc5BHNlYwNNb3N0IFBvcHVsYXIEdmVyA2IwOTg4OTQ0LTZhZjMtMTFlMi1iOTVkLWRkYWFhNzk3NGFlZQ--;_ylg=X3oDMTJsbDNrNmNmBGludGwDdXMEbGFuZwNlbi11cwRwc3RhaWQDBHBzdGNhdANwb3B1bGFyBHB0A3NlY3Rpb25zBHRlc3QDY29udHJvbF9pcHRjX3Nob3J0X3JlbGF0ZWQ-;_ylv=3

[DrDan]

1. having studied mathematics and statistics for a number of years, I appreciate elegance in

in proofs and equations

rare - but, oh, so satisfying

[intaglio]

2. I find Eulers identity wonderful

1+e^i*? = 0

I hope that pi shows up correctly

[pokerfan]

3. It's even more beautiful when expressed using tau

What makes it kind of a kludge is what it's actually describing, i.e. that one ? is only one half a turn so you need to add 1 to get back to zero:

[center]
e ^i? + 1 = 0[/center]

e ^i? is the curved arrow leading to -1 on the horizontal axis.
+1 is the vector leading you from -1 back to 0.

But using a circle constant based upon radius, ?, one can use Euler to now describe one complete turn of the circle returning back to 1.

[center]
e ^i? = 1[/center]

1 tau is 1 turn, not half a turn. Easy and intuitive. Math should illuminate, not obfuscate.

http://tauday.com/

[Geoff R. Casavant]

4. Beauty is in the eye of the beholder, I suppose. I prefer the equation with pi because . . .

. . . it contains the zero, which is itself an important mathematical concept.

[pokerfan]

5. OK, how about this

[center]

e ^i? - 1 = 0[/center]

e^i? is the curved arrow making one complete circuit leading back to +1
-1 is the vector taking you from +1 to 0.

[tama]

8. Thanks

Math is also mystery, and some of the mystery of real part of zeta function being exactly between 0 and 1, according to Riemann (but so far unproven), seems to have something to do with Euler's Identity...

[tama]

7. +1

[struggle4progress]

9. The relation it comes from

e^(i*x) = cos x + i sin x

is even better, since it provides a way to compute many trig identities, such as

sin^2 x + cos^2 x = (cos x + i sin x)(cos x - i sin x) = e^(i*x) * e^(-i*x) = 1

or

cos 2x = (e^(2i*x) + e^(-2i*x))/2 = (e^(i*x)^2 + e^(-i*x)^2)/2 = <-2 + (e^(i*x) + e^(-i*x))^2>/2
= -1 + 2cos^2 x = -sin^2 x - cos^2 x + 2 cos^2 x = cos^2 x - sin^2 x

[pokerfan]

16. Yeah, we EE's get that beaten into our skulls at an early age

along with the Fourier Transform...

[pokerfan]

6. My favorites

Pythagorean Theorem:

[center][/center]
Pythagorean theorem was listed in the OP article but that's one nifty geometric proof.

Maxwell's equations (classical electrodynamics):

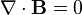
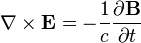
[center]


[/center]
Once described all we knew about electromagnetics and it's still good enough for government work.

Quantum electrodynamics:

[center][/center]
Shout out to Richard Feynman!

Leibniz formula for Pi:

[center]?/4 = 1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 - ...[/center]
It's about the slowest converging series ever but it gets bonus points for its simplicity.

Quadratic factorization:

[center][/center]
I memorized it in grade school and never forgot it.

And then there's this rather surprising one...

[center]e^? - ? = 20[/center]
Commonly used to test the accuracy of floating point operations on calculators.

[struggle4progress]

10. Viewed from a sufficiently advanced PoV the Liebniz formula is by itself a proof

Last edited Thu Jan 31, 2013, 09:31 PM - Edit history (1)

that the so-called Gaussian integers a + bi have unique prime factorization, and this unlocks many facts about Pythagorean triples, because |a + bi|^2 = a^2 + b^2

For example, which ordinary primes appear as the hypotenuse of a right triangle? Exactly the ordinary primes that do not remain prime when considered as Gaussian integers: that is, the prime 2 and the primes of the form 4n + 1

For example, if (a,b,c) is a primitive Pythagorean triple, c has no factor of the form 4n + 3. For, consider the equation a^2 + b^2 = (a + bi)(a - bi) = c^2. If we completely factor a + bi in the Gaussian integers and take the complex conjugate of each factor, we get the factorization of a - bi. The prime factorizations of a^2 + b^2 and of c^2 must be the same. If c has an ordinary prime factor q of the form 4n + 3, q does not factor further, so q appears among the factors of a + ib; then q divides each of a, b, c -- contradicting the fact that (a,b,c) is primitive

And so on ...

Again, if (a,b,c) is a primitive Pythagorean triple, consider the (ordinary) prime factorization of c: c = p1*p2*...*pn. No ordinary prime pj here has the form 4n + 3, so each of these ordinary primes factors in the Gaussian integers: pj = (uj + i*vj)(uj - i*vj). Multiplying
(u1 + i*v1)(u2 + i*v2)...(un + i*vn) = (u + i*v)
we find c = (u + i*v)(u - i*v) = u^2 + v^2. So the hypothenuse of a primitive Pythagorean triple is itself a sum of two squares: that, is, a primitive Pythagorean triple is of the form (a,b,u^2 + b^2) and the Pythagorean theorem in this case looks like
a^2 + b^2 = (u^2 + v^2)^2

Using ordinary arithmetic, it is clear that if (a,b,c) is a primitive Pythagorean triple, then a and b cannot both be even; and if they were both odd a^2 + b^2 would be even (but not divisible by 4), so c^2 would be even (but not divisible by 4), so c would be even, so c^2 would be divisible by 4, a contradiction. Therefore one of the legs is even and the other odd. Interchanging a and b if necessary, we may assume a is odd and b is even. Therefore c = u^2 + v^2 = (u + i*v)(u - i*v) is also odd. Since c is odd, the Gaussian prime 1 + i divides neither (u + i*v) nor (u - i*v). Moreover
(a + ib)(a - ib) = a^2 + b^2 = c^2 = (u^2 + v^2)^2
so the Gaussian prime 1 + i divides neither (a + ib) nor (a - ib). But any Gaussian prime that divides both (a + ib) and (a - ib) must be either an ordinary prime of the form 4n + 3 or the Gaussian prime 1 + i, and so (a + ib) and (a - ib) are relatively prime. Each distinct prime factor of c^2 must therefore appear uniquely in (a + ib) and (a - ib); such a prime factor cannot appear in both. So
(a + ib)(a - ib) = c^2 implies both (a + ib) and (a - ib) are squares, say, a + ib = (x + iy)^2 and a - ib = (x - iy)^2
Writing out
a + ib = (x + iy)^2 = x^2 - y^2 + i*2xy
we have a = x^2 - y^2 and b = 2xy
while
(x^2 + y^2)^2 = (x + iy)^2(x - iy)^2 = (a + ib)(a - ib) = a^2 + b^2 = c^2
gives c = x^2 + y^2
So we recover the ancient Greek formula for primitive Pythagorean triples: they all have the form
(x^2 - y^2,2xy,x^2 + y^2)
where exactly one of x and y is even

[struggle4progress]

11. The last "surprising one" is (of course) seen false, if computed well enough

Even more astonishing is just how very close to an integer exp(pi*sqrt(163)) is

(but it is much more challenging to compute)

[pokerfan]

12. spoilsport

[struggle4progress]

13. oops

sorry



The iteration x <- ln(x + 20) converges pretty quickly to the solution of e^x - x = 20, giving

x = 3.1416333028

[pokerfan]

14. This is a fun read...

http://en.wikipedia.org/wiki/Mathematical_coincidence

Some fun ones...

2^(1/12) * 5^(1/7) = 1.33333319249

? ³²/e²³ = 9.9998387978

[struggle4progress]

15. thanks! that is fun!

[eppur_se_muova]

17. aka Ramanujan's constant ... to see why ...

http://en.wikipedia.org/wiki/Heegner_number#Almost_integers_and_Ramanujan.27s_constant